Na calota da roda de um
automóvel, na bola que enfeita uma árvore de natal e em uma colher de sopa,
podemos ver nossa imagem refletida. Percebemos que essas imagens são diferentes
daquelas formadas nos espelhos planos, podem fornecer imagens aumentadas, ou
diminuídas, maiores ou menores do que o objeto.
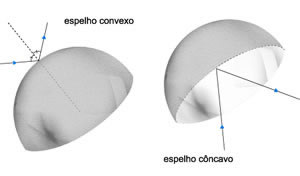
Temos dois tipos de espelho
esférico:
Côncavo: a superfície refletora é interna.
Convexo: a superfície refletora é externa.
Temos:
R ® Raio
de Curvatura;
F ® Foco
do Espelho (ponto médio do eixo principal no trecho entre o Vértice e o
Centro);
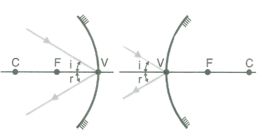
C®
Centro;
V ®
Vértice;
A reta que passa por C e V é o eixo óptico principal.
Condições de Nitidez de Gauss
F
Os raios de luz devem ser pouco inclinados em
relação ao eixo óptico principal;
F
Os raios de luz devem incidir próximos ao
vértice do espelho.
A partir de agora estaremos,
apenas considerando os espelhos esféricos de Gauss
Raios Notáveis de Luz
Os Raios Notáveis não são os
únicos que ocorrem num sistema óptico, mas como o próprio nome diz, eles se
destacam dos outros pela facilidade de traçá-los. Nosso objetivo será desenhar
pelo menos dois deles em cada situação.
Vejamos quais são estes raios:
Todo raio que incide
numa direção que passa pelo centro de curvatura reflete-se sobre si mesmo.
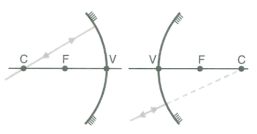
Todo raio que incide paralelamente ao eixo principal
reflete-se numa direção que passa pelo foco principal do espelho.
É importante saber que:
F
O foco F do espelho côncavo é Real;
F
O foco F do espelho convexo é virtual.
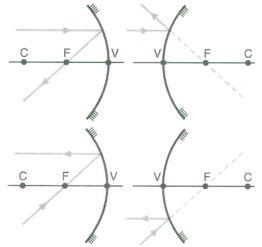
Todo raio que incide numa direção que passa pelo foco reflete-se
paralelamente ao eixo principal.
Esse raio notável decorre do
princípio da reversibilidade da luz.
Determinação Gráfica da Imagem
Para determinarmos graficamente
uma imagem, basta traçarmos dois raios quaisquer de luz entre os notáveis que
acabamos de aprender. Usaremos a notação i e o significando, respectivamente, a
medida da imagem e do objeto.
Espelho
Côncavo
(1) Objeto situado antes do
centro de curvatura C:
(2) Objeto situado sobre o centro
de curvatura C:
(3) Objeto situado entre o centro
de curvatura C e o Foco F:
(4) Objeto situado sobre o Foco
F:
(5) Objeto situado entre o Foco F
e o Vértice:
Espelho
Convexo
Neste caso temos apenas um caso:
Observação:
O espelho convexo é usado como espelho retrovisor de
motocicletas e em portas de garagens devido ao maior campo visual que oferece.
Após tudo o que vimos, podemos
tirar algumas conclusões:
F
Uma imagem real está localizada na frente do
espelho e poderá ser projetada sobre um anteparo (uma tela) colocada na posição
em que ela se forma, pois é constituída pela intersecção dos próprios raios de
luz.
F
Uma imagem virtual está localizada atrás do
espelho e, embora possa ser visualizada, não é constituída por luz e, sim pelos
prolongamentos dos raios.
Determinação Analítica da Imagem
Agora procuraremos expressar de
forma matemática algumas expressões que nos permita determinar a posição e o
tamanho da imagem.
Segundo a figura:
Equação Conjugada de Gauss
O teu Professor fará em sala de aula a demonstração da
equação, aqui apenas apresentaremos esta equação de vital importância na
óptica.
A distância focal é: f = R/2
Aumento Linear Transversal
Por definição, o aumento linear transversal A é a
razão entre a altura da imagem i e a altura do objeto o.
Convenção de Sinais
Objeto
Real => p > 0
Virtual => p < 0
Imagem
Real => p’ > 0
Virtual => p´< 0
Espelho
Côncavo => R > 0 e f > 0
Convexo => R < 0 e f < 0
Altura da Imagem para o > 0
Direita => i > 0
Invertida => i < 0
Aula sobre Espelhos Esféricos




Justo o que eu procurava sobre espelhos, vidraçaria e esquadria de aluminio
ResponderExcluir