Lentes Esféricas

As lentes esféricas constituem sistemas ópticos de amplas aplicações na atualidade. Elas desempenham um papel um papel importantíssimo, desde os sofisticados “LASERS” até os mais simples pares de óculos.

Podemos defini-las como sendo um meio transparente e homogêneo, limitado por duas superfícies curvas, ou por uma curva e outra plana.

A lente será denominada esférica, quando pelo menos uma de suas faces o for. Em caso contrário poderá ser parabólica ou cilíndrica, por exemplo.

Observação:

Uma lente é delgada quando a espessura (e) for desprezível em relação aos raios de curvatura.  (e << R)

8.2 – Classificação das lentes

Podemos classificar as lentes quanto a dois aspectos: tipos de faces e comportamento óptico.

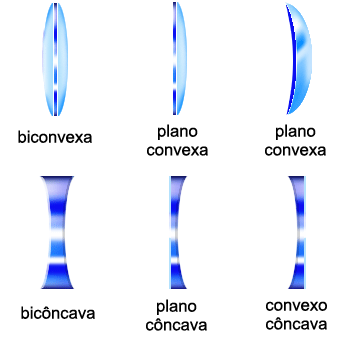
F Classificação quanto as faces:

Observações:

Os nomes das lentes segue a convenção que devemos citar em primeiro lugar a face de maior raio de curvatura.

F Classificação quanto ao Comportamento Óptico:

Nessas figuras consideramos que as lentes são de vidro e estão imersas no ar (n_vidro > n_ar), que é o caso mais comum na prática. Nessas condições, as lentes de bordos finos são convergentes e as lentes de bordos grossos são divergentes.

Raios Notáveis

Assim como foi feito para os espelhos esféricos, iremos agora descrever alguns raios que são fáceis de serem utilizados na determinação da imagem numa lente esférica.

Todo raio que incide no centro óptico atravessa a lente sem sofrer desvio. 

Todo raio que incide paralelamente ao eixo principal emerge numa direção que passa pelo foco.

Todo raio que incide sob o foco emerge paralelo ao eixo principal.

Determinação Gráfica da Imagem

De maneira análoga ao que fizemos para espelhos esféricos iremos proceder agora para lentes.

Determinação Analítica da Imagem

As equações que utilizaremos para a determinação da posição e tamanho da imagem são análogas às utilizadas no estudo de espelhos esféricos.

Regra de Sinais

• p é positivo se o objeto estiver na frente da superfície (objeto real)
• p é negativo se o objeto estiver atrás da superfície (objeto virtual)
• p' é positivo se a imagem estiver atrás da superfície (imagem virtual)
• p' é negativo se a imagem estiver na frente da superfície (imagem real)
• R é positivo se o centro de curvatura estiver atrás da superfície
• R é negativo se o centro de curvatura estiver na frente da superfície

Aula Sobre Lentes Esféricas

Refração Luminosa

Já discutimos o fato da velocidade da luz depender do meio de propagação. A velocidade de uma dada luz monocromática assume valores diferentes em diferentes meios de propagação tais como: vácuo, ar, água, vidro, etc.

A luz sofre refração quando passa de um meio para outro, modificando sua velocidade. Em geral, a refração é acompanhada por um desvio na trajetória da luz, conseqüência da mudança de velocidade. O único caso de refração no qual a luz não sofre desvio é quando incide perpendicularmente à superfície de separação dos meios S.

Os dois meios de propagação, 1 e 2, e a superfície de separação S constituem o que chamamos de DIOPTRO.

Nos dioptros reais, o fenômeno da refração é acompanhado pela reflexão da luz. Assim, o raio de luz incidente na superfície S divide-se em dois raios, um refratado e outro refletido.

É importante também dizer que ocorre em S o fenômeno da absorção da luz, onde parcela da energia luminosa é transformada em energia térmica, por exemplo.

No dioptro ideal só ocorre refração da luz.

Índice de Refração Absoluto

Seja c a velocidade da luz no vácuo e v a velocidade da luz em um meio qualquer, definimos índice de refração absoluto (n) de um meio a razão entre as velocidades da luz no vácuo e no meio considerado:

O índice de refração absoluto do vácuo é naturalmente igual a 1 (v = c). Como a velocidade da luz no vácuo é uma velocidade limite, em qualquer outro meio ela será inferior:

v < c, logo: n > 1

Conclusões:

F O índice de refração absoluto de qualquer meio material é sempre maior que 1.

F Quanto maior for o índice de refração absoluto do meio, menor é a velocidade da luz nesse meio.

Índice de Refração Relativo

Se n_A e n_B são, respectivamente, os índices de refração absolutos dos meios A e B para uma dada luz monocromática, então definimos o índice de refração relativo do meio A em relação ao meio B, n_A,B como sendo a razão dos índices de refração absolutos do meio A e B:

Leis de Refração

Considerando um raio de luz monocromático incidente numa superfície separadora de dois meios de propagação e o correspondente raio de luz refratado. Tracemos a reta normal à superfície pelo ponto de incidência da luz.

Temos:

RI ® Raio Incidente;

RR ® Raio Refratado;

N® Reta Normal;

i ® ângulo de incidência;

r ® ângulo de refração.

1ª Lei: O raio de luz incidente RI, a reta normal N e o raio de luz refratado RR estão situados num mesmo plano (coplanares)

é importante notar que os raios de luz incidente e refratado ficam em lados opostos em relação à reta normal.

2ª Lei ou Lei de Snell - Descartes: É constante a relação entre os senos dos ângulos de incidência e refração.

Podemos escrever que:

Podemos concluir que:

Quando a luz passa de um meio menos refringente (menor índice de refração) para um meio mais refringente (maior índice de refração), o raio de luz se aproxima da normal e a velocidade de propagação diminui.

Reciprocamente, quando a luz passa de um meio mais refringente para um meio menos refringente, o raio de luz se afasta da normal e a velocidade de propagação da luz aumenta.

Aula Sobre Refração no Telecurso 2000

Aula Sobre Refração Luminosa

Exemplos de Refração

Mago da Física - Refração