4 – Teorema de Stevin
Consideremos um
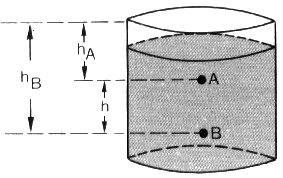
recipiente contendo um líquido homogêneo em equilíbrio estático. As pressões
que o líquido exerce nos pontos A e B são:
p(A) = d . g . h(A)
p(B) = d . g . h(B)
A diferença de
pressão entre os pontos A e B será:
p(B) - p(A) = d . g . h
A diferença entre dois
níveis diferentes, no interior de um líquido, é igual ao produto da sua massa
específica pela aceleração da gravidade local e pela diferença de nível entre
os pontos considerados.
(i) pressão
hidrostática: aquela que só leva em consideração o líquido:
p = d . g . h
(ii) pressão
absoluta: aquela que leva em consideração o líquido e o ar sobre o líquido:
p = patm + d . g . h
Conseqüências do
Teorema de Stevin:
No interior de um
líquido em equilíbrio estático:
(a) Pontos de um
mesmo plano horizontal suportam a mesma pressão;
(b) a superfície de
separação entre líquidos não miscíveis é um plano horizontal;
(c) Em vasos
comunicantes quando temos dois líquidos não miscíveis temos que a altura de
cada líquido é inversamente proporcional às suas massas específicas.
Vasos Comunicantes
d (B) . h (B) = d (A) . h (A)
Exercícios
1> Uma piscina com 5,0 m de profundidade
está cheia com água. Determine:
(a)
a
pressão hidrostática a 3,0 m de profundidade;
(b) a pressão absoluta no fundo da piscina;
(c) a diferença de pressão entre dois pontos
separados, verticalmente, por 80cm.
Considere: g = 10 m/s2 e patm
= 1,0 x 105 Pa
2> A pressão absoluta no fundo de uma
piscina é de 1,4 atm. Logo a profundidade da piscina é de aproximadamente:
(a) 14 m; (b)
0,4 m; (c) 4 m; (d) 0,70 m; (e) n.d.a.
5 – Princípio de Pascal
Pascal fez estudos
em fluídos e enunciou o seguinte princípio:
A pressão aplicada
a um fluído num recipiente transmite-se integralmente a todos os pontos do
mesmo e às paredes do recipiente que o
contém.
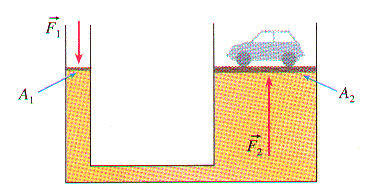
Uma das aplicações
deste princípio é a prensa hidráulica como mostramos a seguir:
Isso mostra que uma
força pequena F1 é capaz de suportar no outro êmbolo um Peso muito
grande (F2), isso é muito utilizado, como por exemplo, em posto de
gasolina.
F1 / A1 = F2 / A2
Exercício
3> Num posto de gasolina, para a lavagem
de um automóvel de massa 1000kg, o mesmo é erguido a uma certa altura. O
sistema utilizado é uma prensa hidráulica. Sendo os êmbolos de áreas 10 cm2
e 2000 cm2 e a aceleração da gravidade local de 10 m/s2,
qual a força aplicada no êmbolo menor para equilibrar o automóvel ?
Vídeo:
Simulação:

Nenhum comentário:
Postar um comentário